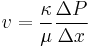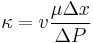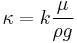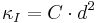Permeability (earth sciences)

Permeability in fluid mechanics and the earth sciences (commonly symbolized as κ, or k) is a measure of the ability of a porous material (often, a rock or unconsolidated material) to allow fluids to pass through it.

Contents

Units

The SI unit for permeability is m2. A traditional unit for permeability is the darcy (D), or more commonly the millidarcy (mD) (1 darcy 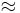\approx10−12m2). The unit of cm2 is also sometimes used (1 m2 = 104 cm2).

Applications

The concept of permeability is of importance in determining the flow characteristics of hydrocarbons in oil and gas reservoirs, and of groundwater in aquifers.

For a rock to be considered as an exploitable hydrocarbon reservoir without stimulation, its permeability must be greater than approximately 100 mD (depending on the nature of the hydrocarbon - gas reservoirs with lower permeabilities are still exploitable because of the lower viscosity of gas with respect to oil). Rocks with permeabilities significantly lower than 100 mD can form efficient seals (see petroleum geology). Unconsolidated sands may have permeabilities of over 5000 mD.

The concept has also many practical applications outside of geology, for example in chemical engineering (e.g., filtration).

Description

Permeability is part of the proportionality constant in Darcy's law which relates discharge (flow rate) and fluid physical properties (e.g. viscosity), to a pressure gradient applied to the porous media:

v = \frac {\kappa}{\mu} \frac{\Delta P}{\Delta x}

Therefore:

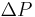\kappa = v \frac{\mu \Delta x}{\Delta P}

where:

v is the superficial fluid flow velocity through the medium (i.e., the average velocity calculated as if the fluid were the only phase present in the porous medium) (m/s)
\kappa is the permeability of a medium (m2)
\mu is the dynamic viscosity of the fluid (Pa·s)
\Delta P is the applied pressure difference (Pa)
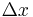\Delta x is the thickness of the bed of the porous medium (m)

In naturally occurring materials, permeability values range over many orders of magnitude (see table below for an example of this range).

Relation to hydraulic conductivity

The proportionality constant specifically for the flow of water through a porous media is called the hydraulic conductivity; permeability is a portion of this, and is a property of the porous media only, not the fluid. Given the value of hydraulic conductivity for a subsurface system, k, the permeability can be calculated as:

\kappa = k \frac {\mu} {\rho g}
where

Determination

Permeability is typically determined in the lab by application of Darcy's law under steady state conditions or, more generally, by application of various solutions to the diffusion equation for unsteady flow conditions.[1]

Permeability needs to be measured, either directly (using Darcy's law) or through estimation using empirically derived formulas. However, for some simple models of porous media, permeability can be calculated (e.g., random close packing of identical spheres).

Permeability model based on conduit flow

Based on Hagen–Poiseuille equation for viscous flow in a pipe, permeability can be expressed as:

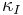{\kappa}_{I}=C \cdot d^2

where:

{\kappa}_{I} is the intrinsic permeability [length2]
C is a dimensionless constant that is related to the configuration of the flow-paths
d is the average, or effective pore diameter [length].

Intrinsic and absolute permeability

The terms intrinsic permeability and absolute permeability states that the permeability value in question is an intensive property (not a spatial average of a heterogeneous block of material), that it is a function of the material structure only (and not of the fluid), and explicitly distinguishes the value from that of relative permeability.

Permeability to gases

Sometimes permeability to gases can be somewhat different that those for liquids in the same media. One difference is attributable to "slippage" of gas at the interface with the solid[2] when the gas mean free path is comparable to the pore size (about 0.01 to 0.1 μm at standard temperature and pressure). See also Knudsen diffusion and constrictivity. For example, measurement of permeability through sandstones and shales yielded values from 9.0x10−19 m2 to 2.4x10−12 m2 for water and between 1.7x10−17 m2 to 2.6x10−12 m2 for nitrogen gas.[3]

Tensor permeability

To model permeability in anisotropic media, a permeability tensor is needed. Pressure can be applied in three directions, and for each direction, permeability can be measured (via Darcy's law in 3D) in three directions, thus leading to a 3 by 3 tensor. The tensor is realized using a 3 by 3 matrix being both symmetric and positive definite (SPD matrix):

The permeability tensor is always diagonalizable (being both symmetric and positive definite). The eigenvectors will yield the principal directions of flow, meaning the directions where flow is parallel to the pressure drop, and the eigenvalues representing the principal permeabilities.

Ranges of common intrinsic permeabilities

These values do not depend on the fluid properties; see the table derived from the same source for values of hydraulic conductivity, which are specific to the material through which the fluid is flowing.

Permeability Pervious Semi-Pervious Impervious
Unconsolidated Sand & Gravel Well Sorted Gravel Well Sorted Sand or Sand & Gravel Very Fine Sand, Silt, Loess, Loam
Unconsolidated Clay & Organic Peat Layered Clay Unweathered Clay
Consolidated Rocks Highly Fractured Rocks Oil Reservoir Rocks Fresh Sandstone Fresh Limestone, Dolomite Fresh Granite
κ (cm2) 0.001 0.0001 10−5 10−6 10−7 10−8 10−9 10−10 10−11 10−12 10−13 10−14 10−15
κ (millidarcy) 10+8 10+7 10+6 10+5 10,000 1,000 100 10 1 0.1 0.01 0.001 0.0001

Source: modified from Bear, 1972

See also

Footnotes

  1. ^ "CalcTool: Porosity and permeability calculator". www.calctool.org. http://www.calctool.org/CALC/eng/fluid/darcy. Retrieved 2008-05-30. 
  2. ^ L. J. Klinkenberg, "The Permeability Of Porous Media To Liquids And Gases", Drilling and Production Practice, 41-200, 1941 (abstract).
  3. ^ J. P. Bloomfield and A. T. Williams, "An empirical liquid permeability-gas permeability correlation for use in aquifer properties studies". Quarterly Journal of Engineering Geology & Hydrogeology; November 1995; v. 28; no. Supplement_2; p.S143-S150. (abstract)

References

External links